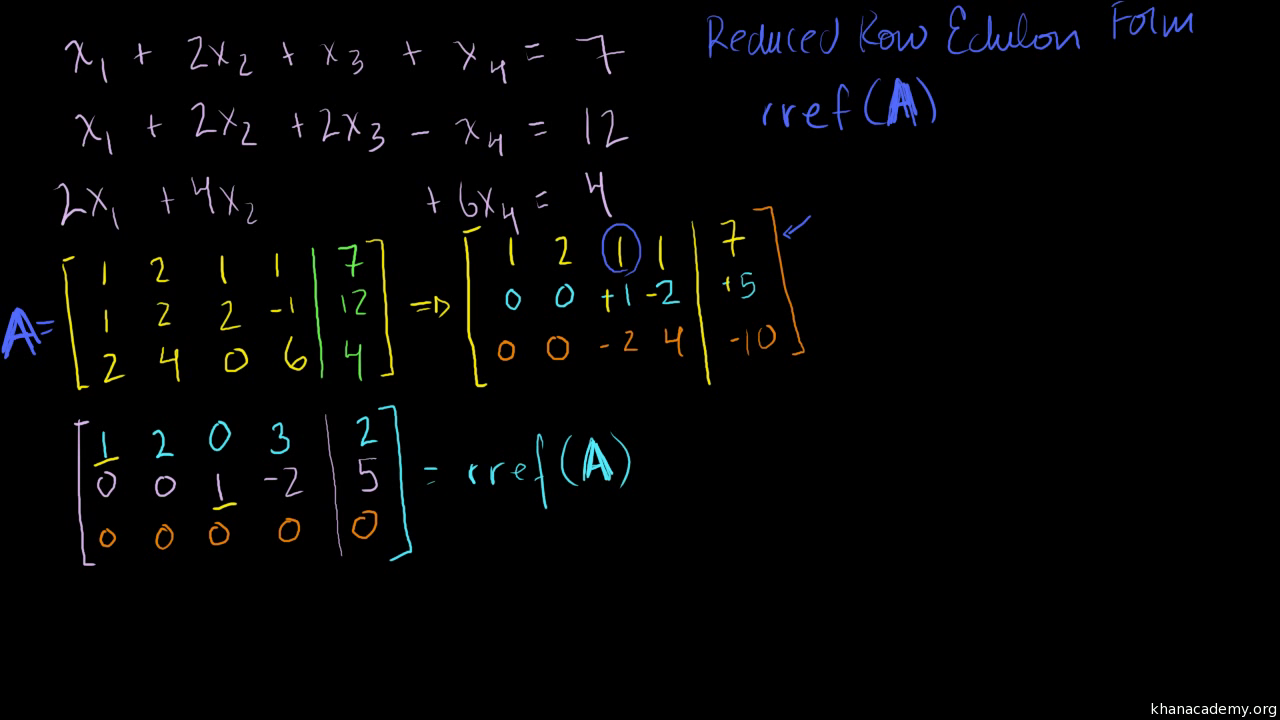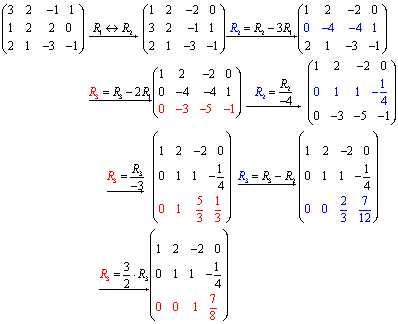Can’t-Miss Takeaways Of Info About How To Reduce Matrix

Making it (188 by 188).

How to reduce matrix. (or possible values of λ) step 3: How to reduce an augmented matrix to row echelon form? Row reduce the augmented matrix.

Thanks to all of you who support me on patreon. You can use sparse matrix to reduce the size: By using a technique in linear algebra called gaussian elimination, a matrix can be systematically shaped into echelon form.

We can find a row that is not. Perform elementary row operations to yield a 1 in the first row, first column. Represent the standardized matrix in its sparse form using.

But remember that k has rank 3, reflecting the rank of a. This online calculator find row reduced form of input. Write the new, equivalent, system that is defined by the new, row reduced, matrix.

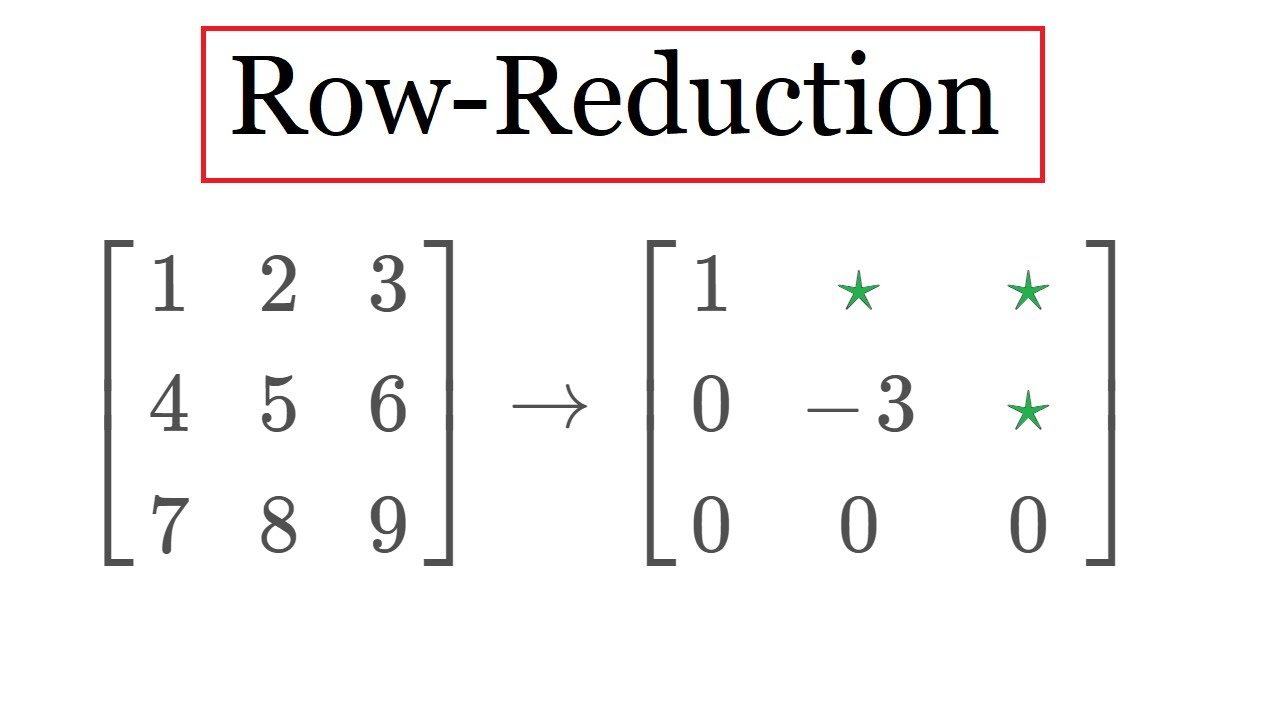
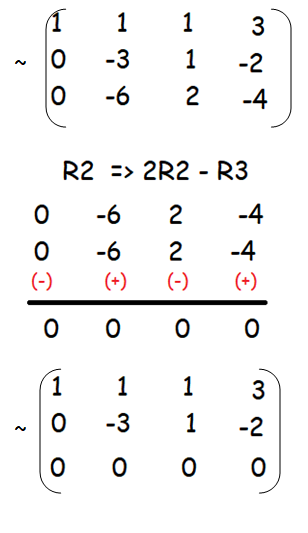
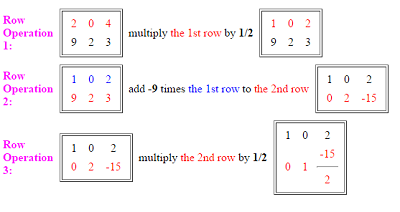
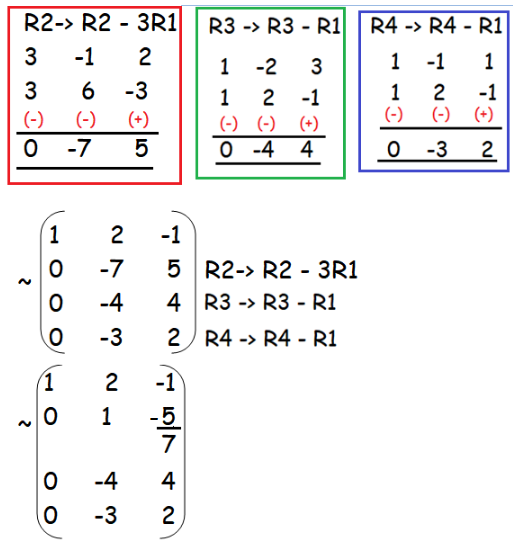
Row reduced matrix called matrix whose elements below main diagonal are equal to zero. If you are first time learning linear algebra, you may find this video very helpful when you need to row reduce a humongous matrix to echelon form (ef) or. To row reduce a matrix:

The matrix row reducer will convert a matrix to reduced row echelon form for you, and show all steps in the process along the way. You can use any of these operations to get a matrix into reduced row echelon form: I would like to then reduce the (1880 x 1880) matrix to every 10th row and every 10th column.

Create zeros in all the rows of the first column except the first row by adding the first. It appears that there are unequal number of zeros in each row so just removing zeros doesn't solve the problem. Write the augmented matrix of the system.

Row reduce the augmented matrix. Each leading entry is in a column to the right of the leading entry in the previous row. Since you don't say exactly what it is that you want to be reduced and what not, i'm just guessing that you want the matrix itself to be smaller.

Multiply each element in a single row by a constant (other than zero). Write the augmented matrix of the system. Find the eigen vectors x 1, x 2, x 3 corresponding to the eigen values λ = 1,2,3.